Projectile motion is found in every physics book but usually its equations are for a projective travelling in vacuum. What about include air drag and solving the resulting differential equation in a very simple way?
Let’s analyse the forces acting on the projectile during its flight. The gravity forces is pulling downwards with a strength of W = m g, where m is the projectile mass and g the gravity acceleration.
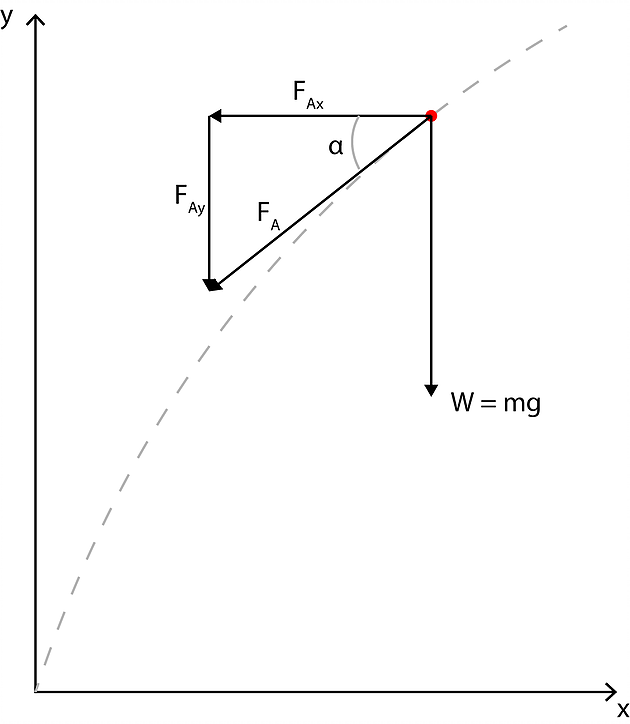
Regarding the aerodynamic drag, it’s proportional to the air density, body surface, and to the velocity squared by means of the proportionality factor CD,
$$
F_A = \frac{1}{2} \rho S C_D (V_x^2+V_y^2)
$$
It is decomposed in horizontal and vertical components
$$
F_{A_x} = F_A \cos \alpha
$$
$$
F_{A_y} = F_A \sin \alpha
$$
where the trigonometric functions are expressed as
$$
\cos \alpha = \frac{V_x}{\sqrt{V_x^2+V_y^2}}
$$
$$
\sin \alpha = \frac{V_y}{\sqrt{V_x^2+V_y^2}}
$$
Applying Newton’s second law which links the sum of forces to the product of mass and time-derivative of velocity, we have a first order differential equations for direction,
$$
\frac{dV_x}{dt} = – \frac{\rho S C_D V_x }{2 m} \sqrt{V_x^2+V_y^2}
$$
$$
\frac{dV_y}{dt} = – \frac{\rho S C_D V_y }{2 m} \sqrt{V_x^2+V_y^2} – g
$$
The trajectory can be easily obtained by noticing that velocity is the derivative of position,
$$
\frac{dx}{dt} = V_x
$$
$$
\frac{dy}{dt} = V_y
$$
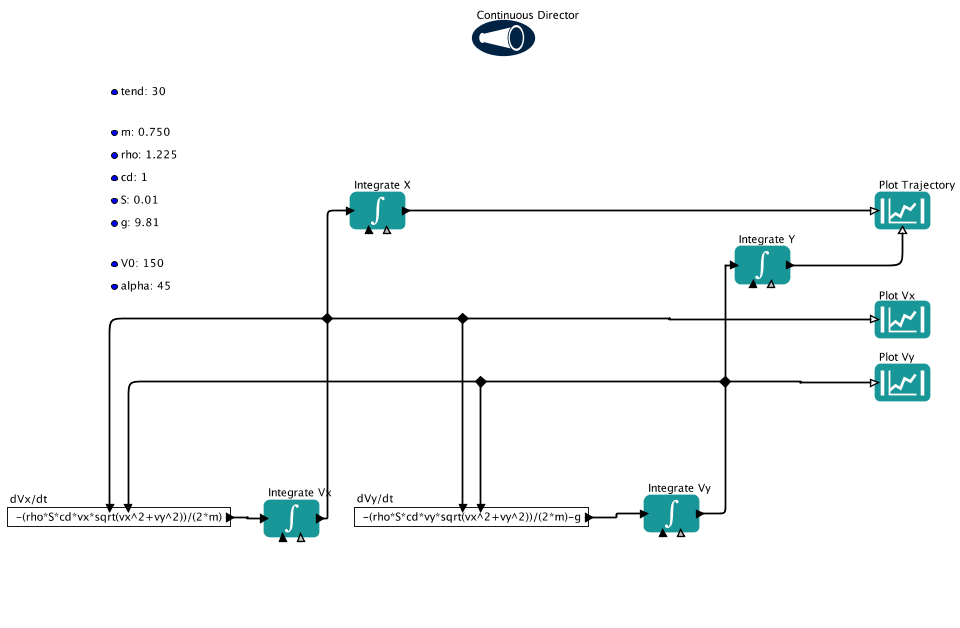
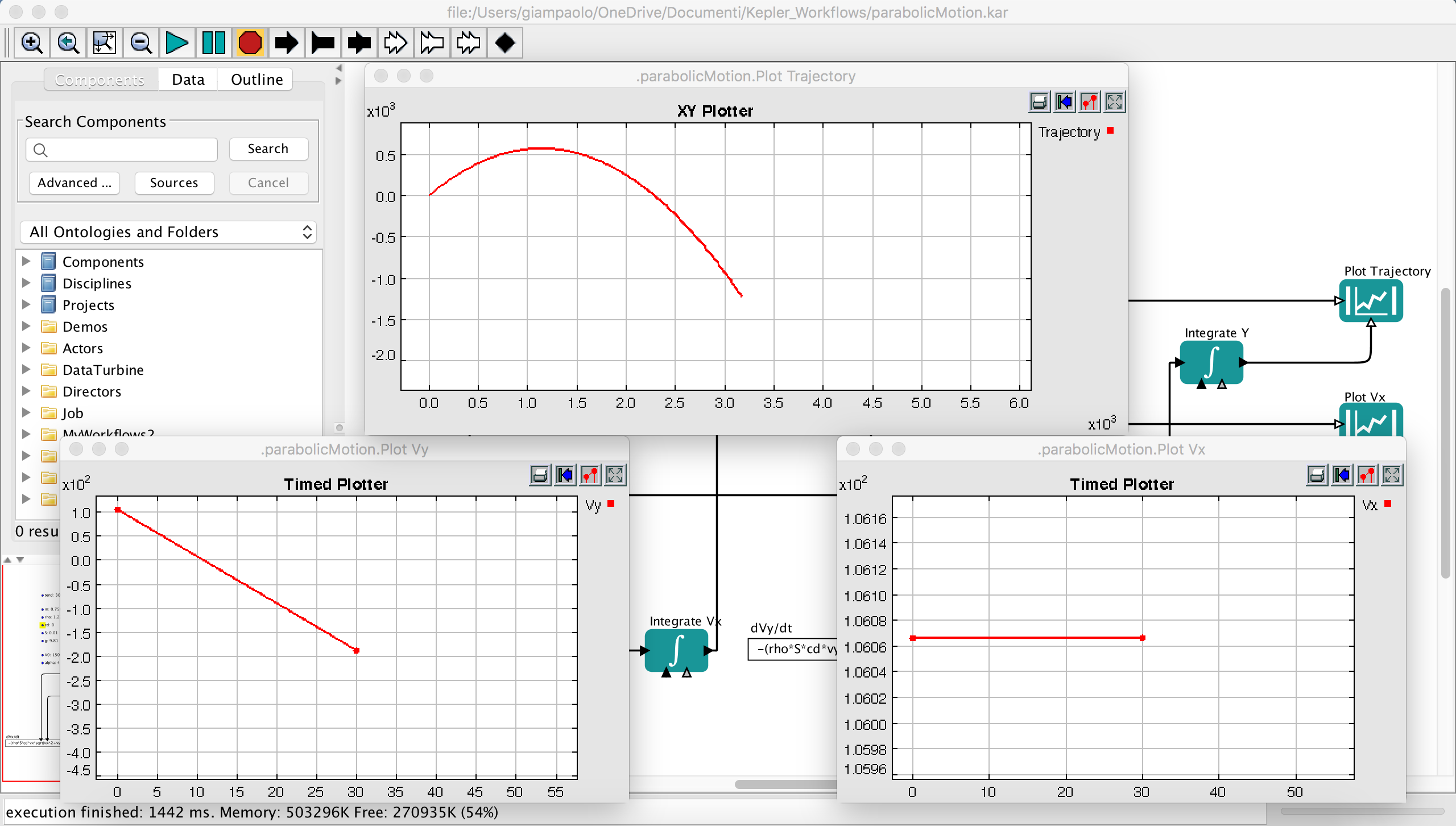
Once we have the equations, we have now to integrate them. We’re going to use a brilliant software called Kepler (official website: kepler-project). It is a software very useful to define scientific workflows by easily drag-and-drop components called “actors”. Solving the set of 4 equations (two for the speed and two for the projectile position) becomes this tidy workflow
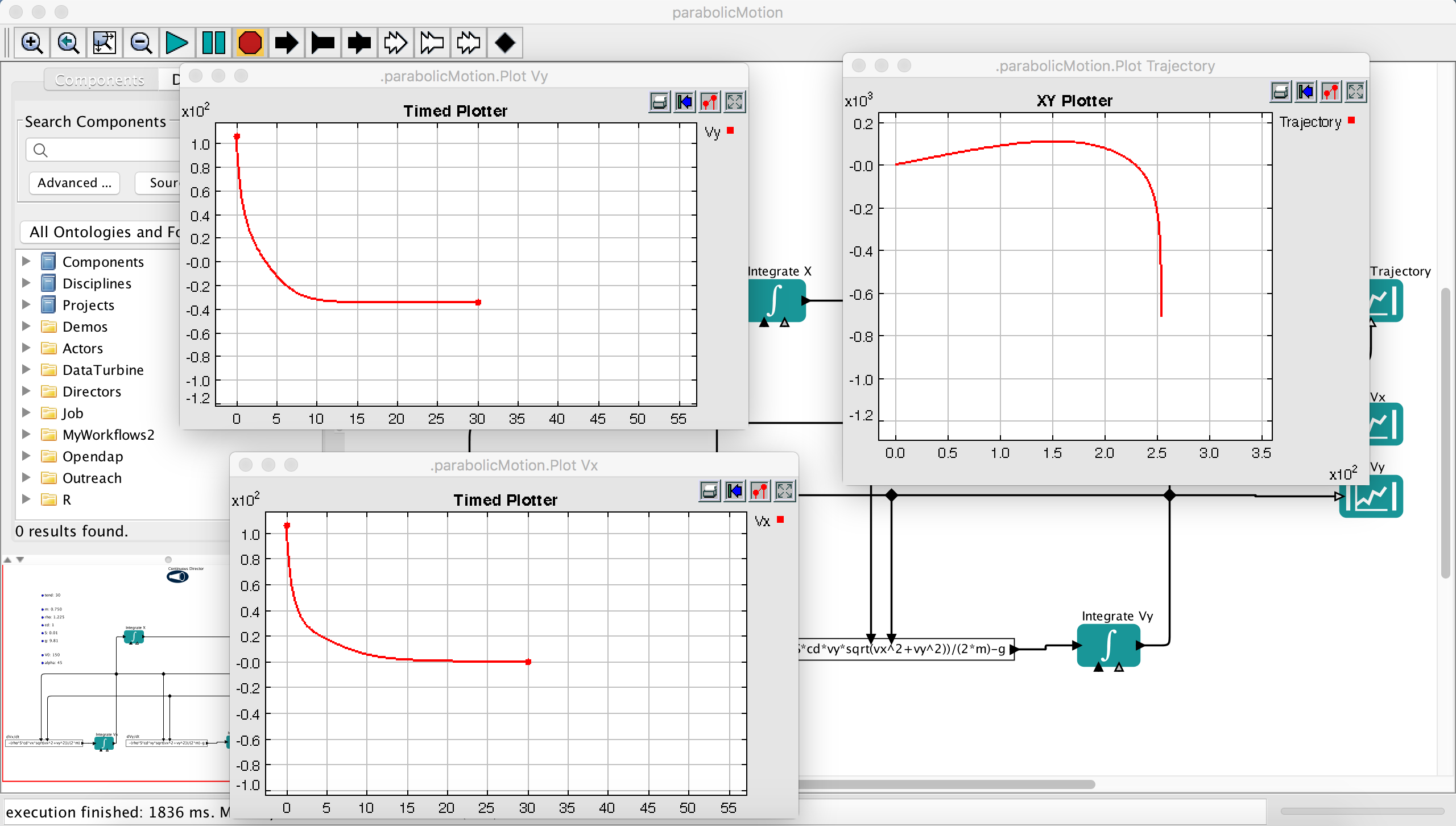
Parameters such as mass and cross surface area are given on the left side while other components are in charge of interactively integrate the equations. When you press the Run button, this is the final results:
where the trajectory is given by the XY Plotter. You can noticing that the projectile starts falling vertically at a certain point and it reaches its terminal velocity.
And now, it’s time to play with parameters! Set CD = 0 to remove any air drag and the results will be
very different, isn’t it? And what’s happening to the vertical speed?
Leave a Reply