Flight dynamics is a fancy name to indicate the study of motion and performance of aircraft. Describing mathematically the motion of aeroplanes is a very complex matter! The starting point is the classical mechanics and the assumption of rigid motion. However, since aeroplanes can accelerate, decelerate, change trajectory and so on, the equations must be written in a particular way.
One of the main problems is the interaction of rigid motions with aerodynamics. For sake of simplicity, let’s assume an aeroplane is flying and starts moving upwards. When the aeroplane starts moving, it changes its position and velocity in respect to the air flow. This affects its aerodynamics and aerodynamics forces change. As a consequence, the motion is influenced by the updated aerodynamics forces. This generates a “loop” which connects motion and aerodynamics.
This coupling between aerodynamics and rigid motions leads to very peculiar effects called aircraft dynamic modes. Let’s stick to the longitudinal plane and the aeroplane can move upwards/downwards, in the left/right direction and rotate in-plane around its centre of gravity. If the pilot try to move the airplane upwards by increasing the thrust and then release the throttle, the aeroplane starts oscillating. These oscillations are very fast and disappear quickly. They arise from the interaction of aerodynamics with vertical and angular velocities. They are so important and well-know that they have a proper name: short period oscillations.
This behaviour can be also simulated using Computational Fluid Dynamics (CFD) to have a very accurate representation of fluid flow. Mathematics is very helpful and with some techniques, it’s possible to identify the mode corresponding to the short period oscillations. Here, I’m animating some results I obtained for a transonic flow and RANS equations. Oscillations are amplified for the animation but you can easily see that they involve vertical and angular velocity.
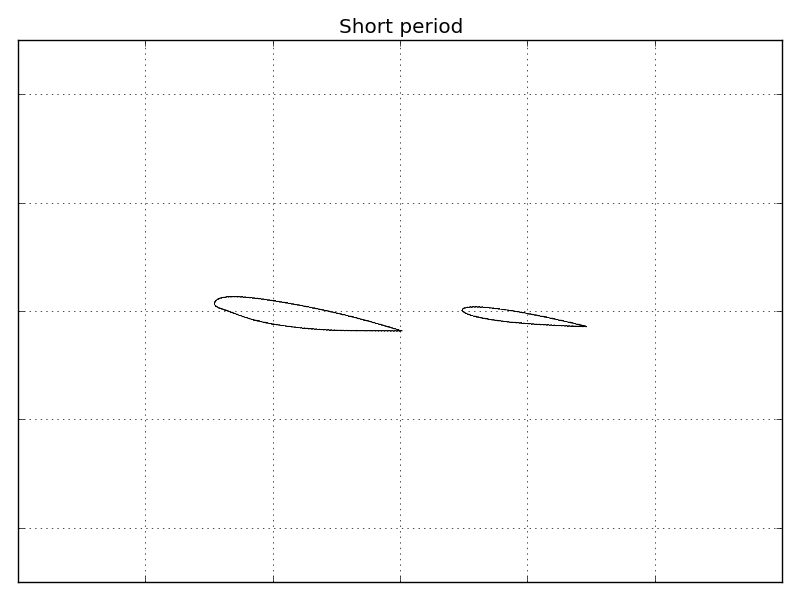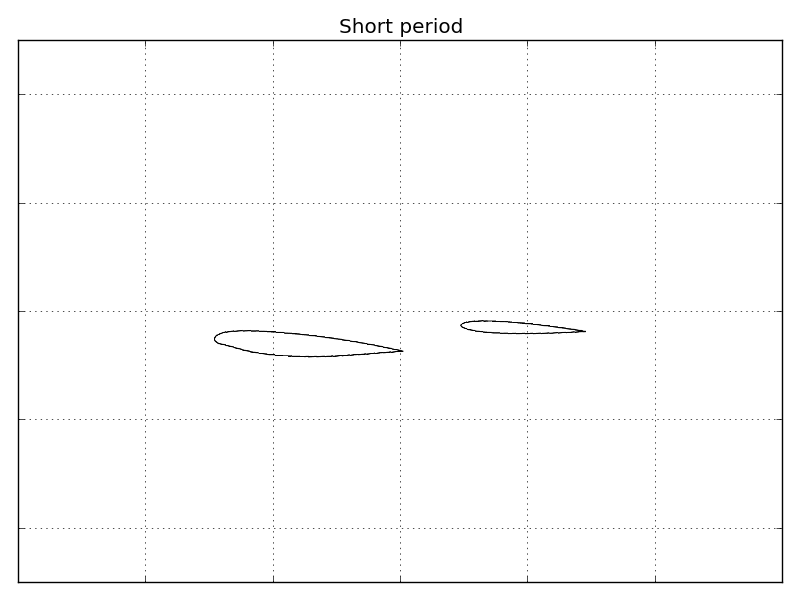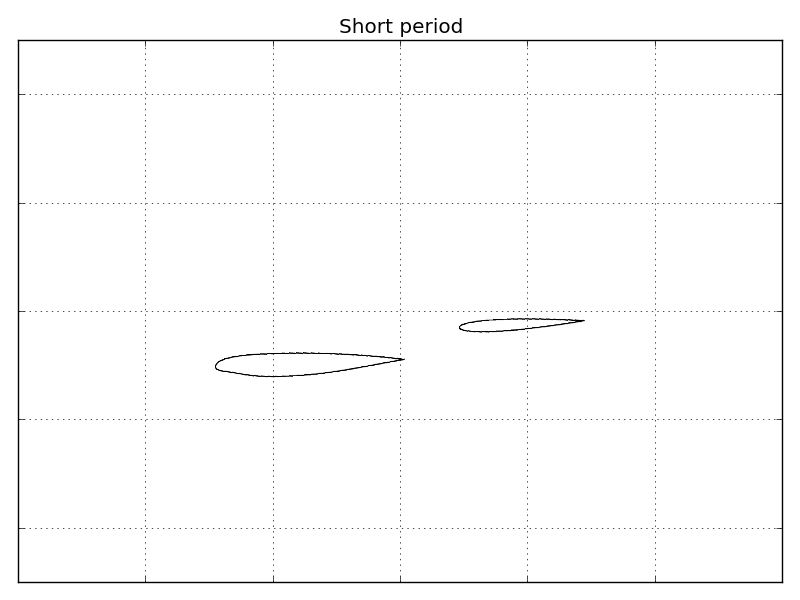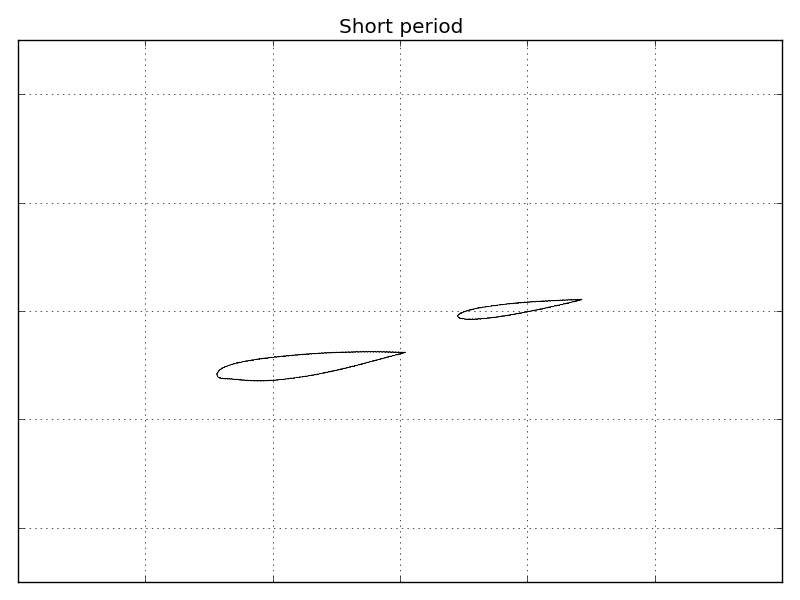
When the short period oscillations have disappeared, a new oscillatory motion become more evident long after the pilot has pulled the throttle. This is a long-term oscillation which affects horizontal velocity and rotation angle. This motion is called phugoid and it depends directly on gravitational acceleration. As a consequence, the phugoid frequency depends on the planet you fly since gravitational acceleration is proportional to the planet mass! This motion is much slower and less damped than the short period.
Similarly to the short period, also phugoid can be animated. In this case I had to speed up the animation to see the phugoid in action!
Differences between the two modes (short period and phugoid) are quite clear from the animations in terms of motion and frequency.
However, it’s very difficult that you’ll feel oscillations resulting from these two modes when flying. In fact, as we said, the short period quickly disappear because of the strong damping. Conversely, the phugoid oscillations have very low frequencies and we need very long time to feel them. During this time, we also need a very quiet environment (no external disturbances) and no actions performed by the pilot. So, next time we fly, we have to pay attention and also hope for a little bit of luck in order to feel the complex dynamics of the airplane!
Leave a Reply